
Maintenant que tu as de quoi lire une vidéo et vérifier vite fait les performances, on va s’attaquer à la première méthode pour la détection des visages. Eh oui, avant de les reconnaitre, il faut déjà les détecter. La première méthode de détection faciale sera avec les cascades de Haar.
Comment ça marche ?
Cette méthode a été publiée par Paul Viola et Michael Jones (pas le guitariste hein) en 2001. Elle consiste à faire glisser un cadre (fenêtre de détection) de gauche à droite et de haut en bas afin de détecter si l’objet qu’on cherche est présent à l’intérieur. Ce cadre se décale d’un pixel vers la droite puis quand il est au bout de l’image, il descend d’un pixel et revient tout à gauche puis recommence son balayage. Ensuite, la fenêtre de détection est agrandie en multipliant ses dimensions par un facteur multiplicatif. Dans la publication de 2001, le facteur multiplicatif était de 1,25. Et on recommence le balayage. Et ce, jusqu’à ce que la fenêtre de détection fasse la taille de l’image. Mais on va voir que grâce à plein de bonnes idées, ce n’est pas si consommateur en calcul que ça.
Les caractéristiques
En fait, pour aller plus vite dans la détection, plutôt que d’utiliser la valeur des pixels, on va utiliser des caractéristiques, c’est à dire une représentation synthétique et informative calculée depuis la valeur des pixels. Cette représentation synthétique va permettre ensuite des calculs plus efficaces et plus rapides.
Et tu vas me demander comment sont calculées ces caractéristiques. C’est simple, les caractéristiques sont calculées en faisant la soustraction des sommes des pixels de zones rectangulaires adjacentes.

Ta tête doit à peu près ressembler à ça en ce moment. Je le sais parce que j’ai eu la même tête avant toi 🙂
En fait c’est simple. Prenons le petit dessin nommé (1) ci-dessous
Maintenant, dans ta tête, dessine sur la photo de Joey, un cadre de 24 pixels par 24 pixels (c’était la taille dans la publication de 2001). Dans ce cadre imaginaire superpose notre petit dessin en noir et blanc. On est d’accord que la partie blanche recouvre la partie gauche et la partie noire recouvre la partie droite. On va faire la somme des pixels de la zone de la photo sous la partie blanche et y soustraire la somme des pixels de la photo sous la partie noire. Hé bien avec cette soustraction, on obtient une caractéristique.
En fonction du résultat du calcul de cette caractéristique, on va pouvoir savoir si ce qu’on cherche est présent ou non. Dans le cas de notre image (1), c’est une caractéristique qui va nous permettre de détecter un bord vertical. Alors, un bord, c’est une image hein. En fait, on va chercher si on voit un changement avec une partie de l’image plutôt claire et une autre plutôt foncée.
Par exemple, pour détecter un nez, on pourrait utiliser une caractéristique comme ça :

Sur les photos, généralement, l’arête du nez est plutôt clair alors que les bords plutôt sombres. On peut donc supposer que si on recherche un visage, cette caractéristique nous sera utile.
Là, tu dois te dire que c’est très consommateur en calcul cette affaire. Alors oui, et c’est pour ça qu’on utilise les “images intégrales”.
Les images intégrales
L’image intégrale est en fait une image de la même taille que notre image de départ mais dont chaque case est composée de la somme des pixels situés au-dessus et à gauche. Voici un petit dessin
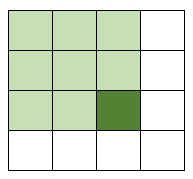
On fait la somme de toutes les cases vert clair (et la case vert foncé) et on met ce chiffre dans la case vert foncé.
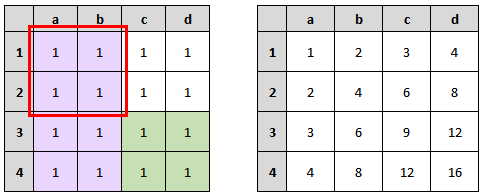
Ok, je te sens toujours dubitatif. Faisons un test avec un exemple concret. Dans le petit dessin ci-dessous, tu as à gauche un tableau représentant une image avec une valeur pour chacun des pixels. Comme je suis nul en math et pour simplifier les calculs qui vont suivre, j’ai mis comme valeur 1 pour tous nos pixels. Dans le tableau de droite, c’est notre image intégrale. C’est à dire avec les sommes de tous les pixels en haut et à gauche.
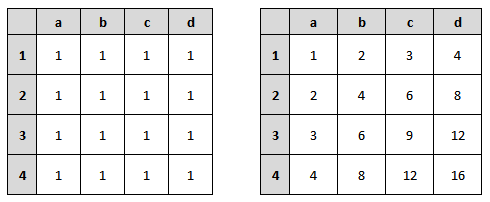
On est d’accord que la case b2 du tableau de droite correspond donc à (a1 + b1 + a2 + b2) du tableau de gauche donc 4.
Maintenant, admettons que je veuille la somme des pixels du rectangle c3-d4 (partie vert clair).
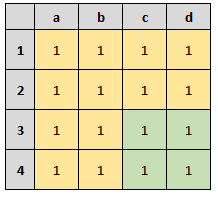
La partie en jaune + la partie en vert c’est la somme de toutes les cases. Donc, la somme de toutes les cases moins la partie en jaune nous donne la somme des cases vertes.
Vu que j’ai mis des 1 partout, on peut le vérifier par le calcul.
Il y a 4×4 cases donc 16 cases donc la somme fait 16.
Il y a 12 cases jaunes et 4 cases vertes.
12 cases jaunes + 4 cases vertes = 16 cases au total.
Donc 16 cases au total – 12 cases jaunes = 4 cases vertes.
Ce qu’aurait dû faire l’ordinateur pour calculer tout ça c’est :
(a1 + b1 + c1 + d1 + a2 + b2 + c1 + c2 + c3 + c4 + d1 + d2 + d3 + d4) - (a1 + b1 + c1 + d1 + a2 + b2 + c1 + c2 + a3 + b3 + a4 + b4) = somme des cases vertes.
Voyons si on peut faire mieux avec notre image intégrale. Prenons l’image ci-dessous.
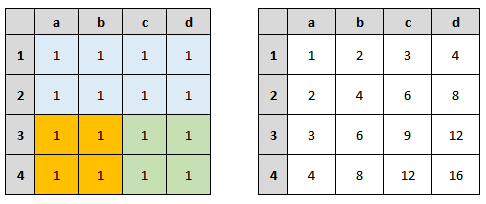
Si je veux reproduire le calcul qu’on a fait plus haut, ça nous donne la formule suivante :
Zone verte = Toutes les cases - zone bleue - zone orange
Est-ce qu’il y a un moyen de connaitre la somme des cases bleues ? Bah oui !! Cette somme est dans notre image intégrale en case d2. La case d2 de notre image intégrale correspond bien à la somme de tous les pixels en haut et à gauche.
Est-ce qu’il y a un moyen de connaitre la somme de toutes les cases ? Toujours oui ! Cette somme est dans notre image intégrale en case d4.
du coup, notre formule devient :
Zone verte = d4 - d2 - zone orange
Bon, il nous reste à trouver une solution pour calculer la somme des cases orange. Regardons l’image ci-dessous.
La zone orange c’est la somme des cases en violet moins la somme des cases dans le rectangle rouge.
Est-ce qu’on connait la somme totale des cases violettes ? Oui, c’est la case b4 de notre image intégrale.
Est-ce qu’on connait la somme totale des cases du rectangle rouge ? Oui c’est la case b2 de notre image intégrale.
Donc la zone orange c’est b4 – b2. On peut le vérifier par calcul, 8 – 4 ça fait 4. Et effectivement la somme des cases orange, ça fait bien 4.
Donc, si on reprend notre formule en remplaçant zone orange par b4 – b2 :
Zone verte = d4 - d2 - (b4 - b2) <=> d4 - d2 - b4 + b2
Vérifions ça :
16 - 8 - 8 + 4 = 4
Effectivement, la somme fait bien 4. Ça veut dire qu’en 4 calculs avec notre image intégrale, on a récupéré la somme des pixels ! Alors qu’il nous fallait beaucoup plus de calcul sans l’image intégrale. Cela va permettre d’accélérer énormément les calculs.
Voilà donc comment faire la soustraction entre la somme des pixels de la zone blanche et la somme des pixels de la zone noire de façon très rapide. Et on remarquera surtout que cette méthode fonctionne quel que soit le nombre de ligne et de colonne ! On utilisera toujours 4 valeurs de notre image intégrale pour faire le calcul.
Et si tu aimes les maths, sache que pour faire la soustraction des sommes des pixels entre 2 rectangles adjacents, il ne faut au total que 6 valeurs de notre image intégrale . Prêt à relever le défi ? 😉
Sélection par boosting
Maintenant, tu vas me dire que des petits dessins en noir et blanc avec 2, 3 ou 4 rectangles adjacents et de différentes tailles, il y en a un certain nombre (plus de 160 000 dans le papier de 2001). Et tous les jouer, ça va être très consommateur en calcul. Oui, mais là encore, il y a une solution.
Nous, on va utiliser un modèle qui est déjà entrainé. Mais durant l’entrainement, toutes les caractéristiques ont été testées sur tout un tas de photo dont le résultat (présence de l’objet) était connu. Du coup, lors de l’entrainement, on a pu cibler les caractéristiques qui servaient à quelque chose de celles qui ne servaient à rien. En 2001, sur les 160 000 de départ, seuls 6000 ont été gardées.
Mais en fait, l’entrainement et la sélection ne vont pas se passer n’importe comment. On va utiliser le système de sélection par boosting.
Prenons une caractéristique et faisons en un classifieur. les résultats possibles sont :
- Je vois quelque chose
- Je ne vois rien
Le but ça va être d’entrainer notre classifieur pour qu’il range au mieux les résultats sans se tromper. Cela consiste donc à trouver la valeur seuil de la caractéristique qui permet de bien ranger correctement dans chacune des boites.
Et on va faire ça pour chacun de nos classifieurs (donc de nos caractéristiques) et en garder que les meilleurs. Ensuite, on va regrouper les meilleurs classificateurs faibles entre eux pour créer ce qu’on va appeler des classificateurs forts.
C’est un peu comme si on disait qu’une chaine météo annonçait du beau temps. Sachant qu’on capte qu’une seule chaine météo, on fait un peu confiance mais bon… Ça reste juste. Maintenant, si on captait 10 chaines météo et que sur les 10, 9 prévoient du beau temps, là, on peut être presque sûr qu’il y aura beau temps.
Je te vois venir. Tu vas me dire que passer de 160 000 à seulement 6000 caractéristiques, c’est bien, mais passer 6000 caractéristiques pour chaque fenêtre de détection, ça reste encore consommateur en termes de calcul.
Et c’est là qu’arrive notre cascade de classifieurs.
Cascade de classifieurs
J’aime bien cette vidéo car elle représente bien ce qui se passe.
Tu auras remarqué qu’il y a des moments où le cadre se déplace vite et des moments où il reste longtemps sur une même zone. Ça, c’est grâce au système de cascade de classifieurs.
Dans notre cas, instinctivement, on imagine un unique gros et puissant classifieur à qui on donne à manger le calcul de nos caractéristiques et qui dit si il trouve l’objet ou pas. Avec cette solution, cela demanderait beaucoup de calcul et d’entrée de jeu un très bon taux de détection. Le problème c’est qu’il faudra le jouer sur chaque fenêtre de détection qui je le rappelle se déplace d’un pixel par un pixel puis qui recommence avec une fenêtre un peu plus grande. Bref, problème.
La solution consiste à faire une cascade de classifieurs plus simple en calcul. Pour être plus précis, on va utiliser nos classifieurs forts créés lors de l’entrainement.
Et c’est là que ça devient intéressant ! En fait, plutôt que jouer tous nos classifieurs forts, on va jouer le premier. On appelle ça un étage. Si celui-ci dit qu’il voit quelque chose, alors on passe au classifieur suivant (l’étage suivant). Sinon, on change de fenêtre de détection. Et le suivant se comportera de la même façon. S’il voit quelque chose, alors, il le passe encore à un autre étage, sinon on change de fenêtre de détection. Et ainsi de suite.
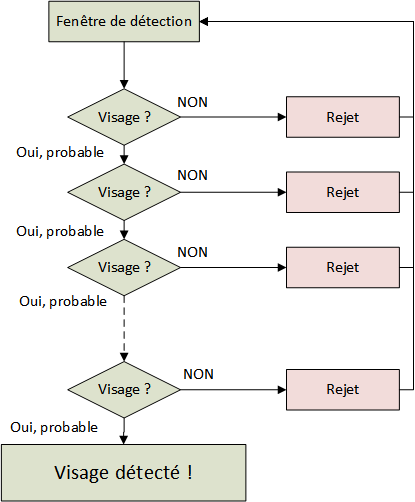
L’idée est que l’immense majorité des fenêtres testées ne contiennent pas l’objet, on passe à la fenêtre suivante plus rapidement, et donc on limite le nombre de calcul à faire.
Mais si tous les étages disent qu’ils voient quelque chose, alors banco ! on déclare le visage dans notre fenêtre de détection.
C’est pour ça que dans la vidéo ci-dessus, on voit parfois notre fenêtre de détection se déplacer très vite. Dès le début, notre fenêtre de détection est rejetée dès les 5 ou 6 premiers étages. Alors que lorsqu’elle est sur le visage, cela prend un peu plus de temps, car on passe par tous les étages. J’en vois 22 dans la vidéo vers 1min 7 seconde.
Dans quel ordre ?
Vu que notre fenêtre de détection doit potentiellement passer par tous nos étages, l’organisation des étages est importantes. L’objectif est de faire le moins de calcul possible.
Pour ça, on a besoin de rappeler ce qui se passe dans un classifieur de façon générale. On lui donne à manger une info et il nous donne un résultat. Dans notre cas, le résultat ne peut avoir que 2 valeurs :
- Je vois
- Je ne vois pas
Mais ce n’est pas pour autant que le résultat est le bon ! C’est ce que lui pense être le bon résultat. du coup, on se retrouve avec 3 situations possibles.
- La première situation c’est que notre classifieur ne s’est pas trompé. Il dit “Je vois” et effectivement il y a quelque chose à voir (ou je ne vois pas et il n y a rien à voir). On appelle ça un “Vrai positif“.
- La deuxième situation c’est que notre classifieur dit “Je vois” alors qu’il n y a rien à voir. Le résultat est faux et on appelle ça un “Faux positif“.
- La troisième situation c’est que notre classifieur dit “Je ne vois pas” alors qu’il y a quelque chose à voir. Ça, c’est plus grave. On appelle ça un “Faux négatif“.
Pourquoi le cas 3 est le plus grave ? Prenons notre étage 1 et supposons qu’il n y a rien à voir.
Si c’est le cas 1 qui arrive, nickel, on est content. Si il n’y a réellement rien à voir, on passe à la fenêtre de détection suivante, on a gagné beaucoup de temps de calcul.
Si c’est le cas 2, c’est à dire qu’il croit voir quelque chose alors qu’il n y a rien, qu’est-ce qu’il se passe ? Il donne la fenêtre de détection à l’étage suivant. Et peut-être que cet étage 2 lui constatera qu’il n’y a rien à voir et donc on passera à la fenêtre suivante. Au fond, on a perdu un peu de temps de calcul mais ce n’est pas si grave.
Mais si c’est le cas 3, c’est à dire que notre étage dit “Je ne vois pas”, alors qu’il y a quelque chose à voir, on vient de rater une détection. Et ça, il faut bien évidemment l’éviter à tout prix.
En résumé, on va s’autoriser un taux de faux positif “élevé”, c’est à dire que le cas où l’étage dit “Je vois” alors qu’il n’y a rien à voir. Car on se dit que l’étage suivant corrigera peut-être l’erreur.
On va donc chercher à privilégier la situation où notre étage dit “Je ne vois pas” et qu’il ne se trompe (presque) jamais. Cela permet de passer à la fenêtre suivante.
Et c’est lors de l’entrainement qu’on va sélectionner et entrainer les caractéristiques pour coller au mieux à ce comportement.
Et l’organisation alors ?
J’y viens ! Maintenant qu’on sait un peu comment ça fonctionne, on sait quels classifieurs on va mettre dans les premiers étages. On va mettre des classifieurs dont le calcul est plus simple et donc plus rapide. Car ce qui va se passer c’est qu’avec un calcul simple et rapide, si le résultat est “Je ne vois pas”, alors c’est (presque) sûr qu’il n’y a rien à voir. On aura donc éliminé notre fenêtre de détection avec un temps de calcul très réduit 🙂
Et pour réduire encore un peu plus le temps de calcul, dans les premiers étages, on ne va pas mettre beaucoup de caractéristiques. Dans le papier de 2001, les auteurs avaient mis 1,10,25,25 et 50 caractéristiques dans les 5 premiers étages.
Lors de l’entrainement, nos étages sont entrainés avec ce qui a réussi à passer l’étage d’avant. En gros l’étage 2 s’entraine car l’étage 1 à dit : Je vois quelque chose. Mais attention ! Ce n’est pas parce que l’étage 1 a vu quelque chose, qu’il y a réellement quelque chose ! C’est peut être un faux positif. Si c’est le cas, ça veut dire que notre étage 2 fait potentiellement face à un problème un peu plus difficile qu’à l’étage 1. Et l’étage 3 encore un peu plus que l’étage 2 etc.
Fusion des détections multiples
Il reste quand même un problème. Si on détecte un visage dans une fenêtre de détection et qu’on décale ensuite notre fenêtre d’un pixel, il y a fort à parier qu’il détectera à nouveau le visage.
D’ailleurs, on le voit bien dans la vidéo, il y a plusieurs cadres rouges car le visage a été détecté plusieurs fois. Hé bien on fusionnera les rectangles qui sont très proches en termes de coordonnées pour n’en faire plus qu’un.
En résumé
Bon, on va essayer de résumer tout ça. Une fenêtre de détection se décale donc pixel par pixel puis grandit jusqu’à faire toute l’image.
Au sein de cette fenêtre de détection, il va y avoir une cascade de classifieurs qui réagira quand elle verra un visage.
Cette cascade de classifieurs est composée de caractéristiques qui réagissent lorsqu’elles voient ce qu’elles pensent être une partie du visage.
Notre cascade s’exécute séquentiellement, c’est à dire que si l’étage 1 voit quelque chose, on passe notre fenêtre de détection à l’étage 2, sinon on change de fenêtre de détection. Si l’étage 2 voit quelque chose, on passe à l’étage 3 sinon on change de fenêtre de détection. etc.
Le but est d’éliminer très vite les fenêtres de détection dans lesquelles il n’y a pas de visage pour économiser du temps de calcul.
Si tous les étages voient un visage, alors, il y a détection de visage.
Voilà, j’ai essayé de ne pas faire trop long mais je tenais quand même à t’expliquer ce qui se passe un peu derrière tout ça. Au final, ce n’est pas si compliqué à comprendre. Alors, j’ai un peu simplifié les choses, mais dans les grandes lignes, tout est là 🙂

Poster un Commentaire